As part of a $10 million center grant from the Institute of Education Sciences, Nancy C. Jordan, professor of learning sciences in UD’s School of Education, Lynn Fuchs of Vanderbilt University, and Robert Siegler of Carnegie Mellon University, created The Center for Improving the Learning of Fractions (CILF) to develop a better understanding of why elementary school children struggle with fractions.

The multidisciplinary research team identified fractions as a crucial aspect of mathematics education in the intermediate grades.

“Research has shown that fractions are a gateway to understanding algebra, which is key to success in higher-level mathematics and for those entering the STEM workforce,” says Jordan. “However, fractions are not only important for math achievement in school, but also for everyday life in preparing foods, calculating mortgage rates and even making health care decisions.”

To address these learning difficulties in mathematics, the Center committed to a focused program of research including a longitudinal study of elementary and middle school children and the development of an intervention.

Longitudinal study to identify key predictors

From 2010 to 2014, the Delaware Longitudinal Study of Fraction Learning followed over 500 children in two school districts to examine fraction development between third and sixth grade, the primary instructional period for teaching fractions to students. The goal was to identify key predictors of learning difficulties in fractions as well as the relation of growth in fraction knowledge to later mathematics difficulties. Jordan and her CILF colleagues chose to oversample participants from schools serving low-income communities, since they were especially interested in children with or at risk for learning difficulties.

The researchers, who included CEHD alumni Nancy Dyson, Ph.D. ’11, Nicole Hansen, Ph.D. ’15, and Jessica Carrique, an SOE graduate student, found a number of predictors of fraction difficulties ranging from specific mathematical skills to executive functions. Though the research team is continuing to analyze their data, a few important findings are already available:

• Third grade predictors of fourth grade fraction outcomes: After controlling for background variables of age, gender, and income status, Jordan and her colleagues found that a third-grader’s ability to estimate the placement of whole numbers on a number line was the most important predictor of success in general fraction concepts and fraction procedures at the end of fourth grade. Children with a clear understanding of whole number magnitude performed better in the early stages of learning fractions. Attentive behavior and verbal ability also contributed to success with early fractions.

• Fifth grade predictors of sixth grade fraction outcomes: For students entering sixth grade, significant predictors of success with fractions included a mastery of whole number line estimation, long division skills, attentive behavior and working memory. Non-symbolic proportional reasoning—the ability to visualize relationships between equivalent fractional quantities—was also an important predictor. For example, fifth grade students who understand that eight cookies for four people is proportionally the same as 16 cookies for eight people, perform better with fractions in sixth grade.

The team also found that a significant number of struggling children shows little growth in fraction knowledge. This struggle with fractions predicts later mathematics failure. For example, 42% of students in the study struggled with accuracy in estimating fraction magnitude and showed minimal growth by the end of sixth grade. When assessed, 67% of this group did not meet state mathematics standards.

“There’s a substantial group of children who make very little progress during the course of fraction instruction. Even at the end of sixth grade, they don’t have a good sense of the meaning of a fraction and have difficulty comparing fraction magnitudes,” says Jordan. “Many children still think about fractions as being something smaller than one, even though a fraction can represent any size.”

Developing an intervention

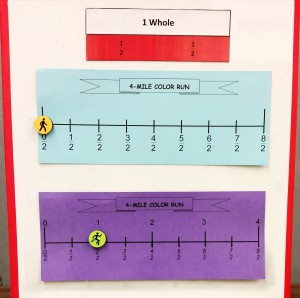In response to these findings, Jordan and her team are developing a fraction sense intervention aimed at building robust knowledge of fraction magnitudes in struggling learners. The invention focuses on ordering fractions on a number line and emphasizes the relationship between the numerator and the denominator. In its current stage, intervention instructors, who have been trained in the fraction sense approach, work with small groups of children in school during their designated intervention time.

In this novel approach, the research team teaches fraction sense components with only a small set of denominators to deepen understanding, and they anchor the instruction in a meaningful storyline to help students think about fractions in a real-world context. For example, using a number line from 0 to 2 to display a 2-mile color run, the team can demonstrate that 4/2 is the same as 2 miles or 4 half miles, or that 1/4 of a mile is farther than 1/5 of a mile. The intervention also uses general principles from cognitive science, including the use of gestures, to guide students’ attention to critical aspects of problems.

Jordan and her team conducted a field trial with a group of seventh-grade students who struggled specifically with understanding fractions. Twenty-one of these students received the fraction sense intervention from project-trained instructors. The control group of 23 students received the intervention instruction already in place at the school.

The fraction sense instructors met with small groups of students for a total of 14 30-minute lessons. Preliminary analysis of the intervention shows significant improvements in the students’ understanding of fraction magnitudes, fraction concepts, and fraction procedures (the calculation of fractions). Significantly, the intervention group continued to outperform the control group eight weeks after the intervention ended.

Next steps

As a next step in this project, Jordan and her team have submitted grant proposals to continue the intervention development, expand the field test, and measure the intervention’s efficacy.

“If the intervention is effective, we hope to understand the mechanisms of change and to train teachers to carry out the intervention in an authentic school setting. An intervention isn’t useful if teachers feel that they cannot implement it successfully,” said Jordan. “We hope to work with teachers, first in a co-teaching, research-teacher collaboration, and then see if the intervention can be carried out successfully by intervention teachers in schools.”

Related references

Bailey, D.H., Zhou, X., Zhang, Y., Cui, J., Fuchs, L., Jordan, N. C., Gersten, R., & Siegler, R.S. (2015). Development of fraction concepts and procedures in U.S. and Chinese children. Journal of Experimental Child Psychology, 129, 68-83. doi: 10.1016/j.jecp.2014.08.006

Fuchs, L. S., Schumacher, R. F., Long, J., Namkung, J., Hamlett, C. L., Cirino, P. T., Jordan, N. C., Siegler, R. S., Gersten, R., & Changas, P. (2013). Improving at-risk learners’ understanding of fractions. Journal of Educational Psychology, 105(3), 683-700. doi:10.1037/a0032446

Hansen, N., Jordan, N. C., & Carrique, J. (2015). Identifying learning difficulties with fractions: A longitudinal study of student growth from third through sixth grade. Contemporary Educational Psychology.

Hansen, N., Jordan, N. C., Siegler, R. S., Fernandez, E., Gersten, R., Fuchs, L., & Micklos, D. (2015). General and math-specific predictors of sixth-graders’ knowledge of fractions. Cognitive Development, 35, 34-49. doi:10.1016/j.cogdev.2015.02.011

Jordan, N. C., Hansen, N., Fuchs, L. S., Siegler, R. S., Gersten, R., & Micklos, D. (2013). Developmental predictors of fraction concepts and procedures. Journal of Experimental Child Psychology, 116(1), 45-58. doi:10.1016/j.jecp.2013.02.001

Jordan, N. C., Kaplan, D., Ramineni, C., & Locuniak, M. N. (2009). Early math matters: Kindergarten number competence and later mathematics outcomes. Developmental Psychology, 45(3), 850-867. doi:10.1037/a0014939

Resnick, I., Jordan, N. C., Hansen, N., Rajan, V., Rodrigues, J., Siegler, R. S., & Fuchs, L. (in press). Developmental Growth Trajectories in Understanding of Fraction Magnitude from Fourth through Sixth Grade, Developmental Psychology.

Siegler, R. S., Fuchs, L., Jordan, N., Gersten, R., & Ochsendorf, R. (2015). The center for improving learning of fractions: A progress report. In S. Chinn (Ed.), The Routledge International Handbook of Dyscalculia and Mathematical Learning Disabilities (pp. 292-302). London: Routledge.

Article by Jessica Henderson

Photo courtesy of Nancy Jordan